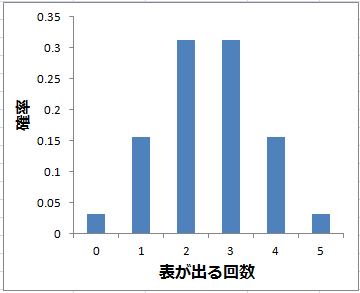
前回やったコイントスの例を思い出そう。例えば,5回コインを振って,表の出る回数ごとの確率分布をグラフにすると,下図のようになる。

この例で,だんだんコインを振る回数を増やしていくと,分布はどのようになっていくだろうか。本当にやると日が暮れるので,BINOMDIST関数を利用して試してみよう。
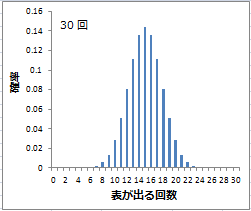 | 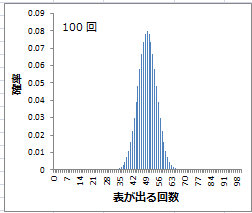 |
| 試行回数30回 | 試行回数100回 |
だんだんx軸の間隔が詰まってきて,分布の形が釣鐘型になってきているのがわかる。これをさらに増やして「無限回」とすると,x軸には「無限個」のデータが詰まることになる。
連続な値を取る確率変数を「連続確率変数」と呼ぶ。上のコイントスの例で「試行回数を無限回にした場合」は,表が出うる回数も無限個あるのだから連続確率変数となる。また,例えば「身長」は,連続的にジワーッと伸びるので,飛び飛びの値にはならない。これも連続確率変数である。
連続確率変数の確率分布は下の左側の図のようになめらかな曲線となる。しかし,二項分布の時と違って,連続確率変数が取りうる値は「無限個」ある。このため,それぞれの値が取る確率の合計が 1 となるように,ある1つの値が取る確率を決めることができない。確率は「確率変数のある範囲の面積」として表され,-∞から+∞までの面積が 1 となる(下図左)。このような確率分布を与える関数を「確率密度関数」と呼ぶ。一方,「ある値までの累積確率」を与える関数を「確率分布関数」と呼ぶ(下図右)。確率分布関数を微分すると確率密度関数が得られる。
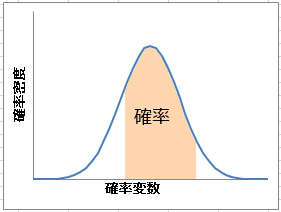 | 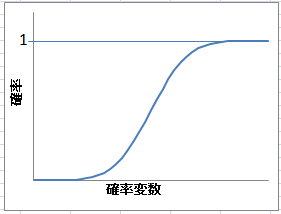 |
| 確率密度関数のグラフ | 確率分布関数のグラフ |
連続確率分布の中で最も重要なのが正規分布である。上の項で示した確率密度関数と確率分布関数のグラフは,共に正規分布のグラフである。
確率変数Xが正規分布する時,その確率密度関数 f(x) は,平均μと分散σ2(標準偏差σ)を用いて下式で与えられる。正規分布する集団は,一般的に N(μ,σ2) と表される。
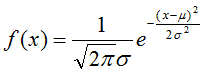
正規分布は,観測誤差や身長など,多くの実データをよく近似できることが示されている。上で試した「コイントスの試行数をどんどん増やしていった場合」も,正規分布に近づいていく。
また,正規分布は今後学ぶ統計的検定の基礎ともなっている。
正規分布は平均μと標準偏差σで決まるので,正規分布するデータでは,ある値が以下の範囲に入る確率も決まっている。便利なので数字のまま覚えておくとよい。
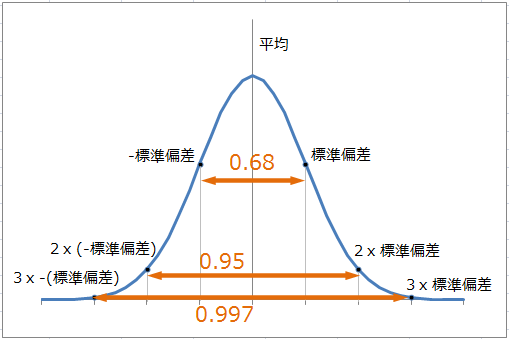
Excel では,正規分布における確率を求める NORMDIST 関数が用意されている。書式は以下の通り。
=NORMDIST(確率変数xの値,平均,標準偏差,関数形式)
「関数形式」は,通常は TRUE を指定する。TRUE を指定すると,データがx以下に入る確率を返す(確率分布関数の値を返す)。この値は度数分布表における「相対累積度数」に相当する。FALSE を指定すると確率密度を返す(確率密度関数の値を返す)。
正規分布は,観測誤差や身長など,多くの実データを近似できることが示されている。例えば,第2回で作成したプロ野球選手のヒストグラムを見直してみよう。
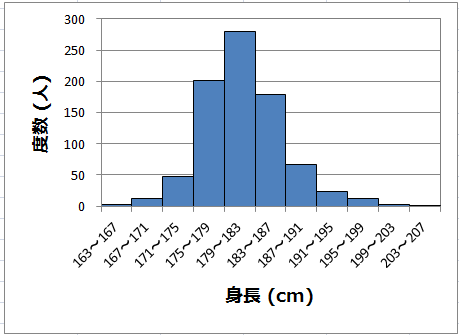
データから身長の平均値と分散を算出すると,平均μ=181.0,標準偏差σ=5.3 である。平均181.0,標準偏差5.3の正規分布において,各階級の値が出現する確率を,NORMDIST関数で求めて,実際の分布と比較してみよう。
ヒストグラムに重ねてみると,下図のようになる。プロ野球選手の身長は,正規分布で非常に良く近似できることがわかる。
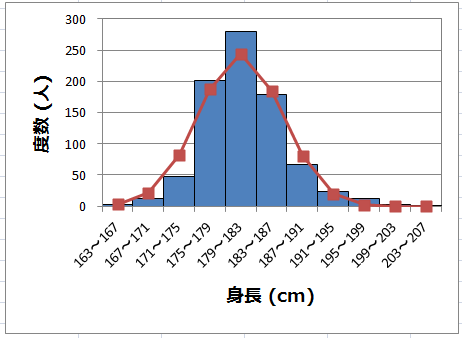
ということは,μ±2σの区間にだいたい95%のデータが入るのだから,プロ野球選手のだいたい95%くらいの人が,身長170.4cm〜191.6cmの間に入る,ということである。
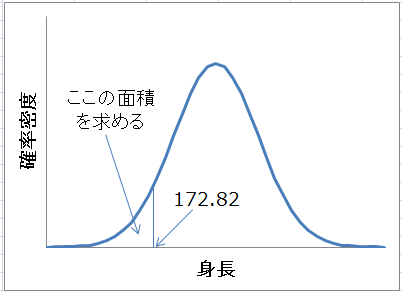
総務省統計局で公開されている『体力・運動能力調査』の2010年度版データによると,20〜24歳の日本人男性の平均身長は172.82cmだそうだ。ということは,この年齢の日本人男性なら,およそ半分の人が172.82cmを下回るということである。
さて,プロ野球選手の平均身長は181cmとかなり大きい。身長172.82cm以下の人は何%くらいなのだろうか。プロ野球選手の身長は正規分布でよく近似できているので,NORMDIST関数を使って推定しよう。
=NORMDIST(172.82,181.0,5.3,TRUE)
ここで求められる確率は,下図のように身長≦172.82 となる部分の面積に相当する。