アパートの家賃(2)

ダミー変数を用いた重回帰分析

前回の例題では，目的変数を家賃として，面積，築年数，駅歩を説明変数にして，重回帰分析を行ったが，方位や構造といった情報は利用しなかった。南向きかどうかとか，鉄骨であるかどうかといったことは，家賃に影響を与えているように思える。しかし，方位や構造のような質的データはそのままでは重回帰分析を行うことができない。そこで，方位を重回帰分析にかけるために，南向きなら1，そうでなければ0というように数値に変換した変数を用意すればよい。このような変数をダミー変数と呼ぶ。

構造については，「鉄骨造」，「軽量鉄骨」，「木造」という3つのカテゴリーがあるが，このような場合には，ダミー変数を2つ用意して（例えばX1とX2とする），下表のように値を設定すればよい。

構造X1X2
鉄骨造1 0
軽量鉄骨01
木造00

カテゴリーが k種類あれば，k-1個のダミー変数を用意する。上の例でダミー変数を一個だけ用意して，鉄骨=0，軽量鉄骨=1，木造=2のようにしてはいけない。

データ準備

前回の使用したデータで，「駅徒歩分」と「間取」の間に3列挿入し，「南向き」，「鉄骨造」，「軽量鉄骨」というダミー変数を用意しよう。

回帰分析

「データ」→「データ分析」で「回帰分析」を選び下図のように指定してOKボタンをクリック。

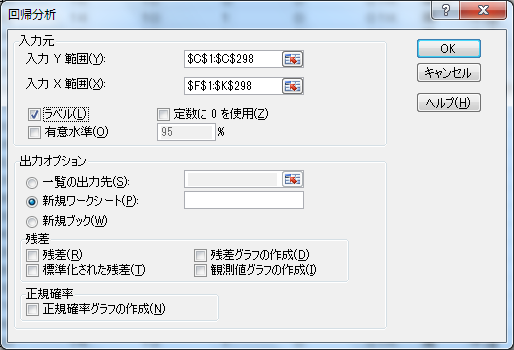
重回帰分析の結果をみてみよう。

回帰係数推定結果

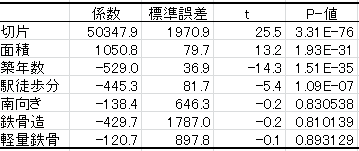
結果をみると，南向きの物件は，そうでないものに比べて138円安くなり，鉄骨造の物件は，そうでないものに比べて430円も安くなるという結果となった（軽量鉄骨も120円安くなる）。しかし，各ダミー変数の係数のP-値を見てみると，いずれも0.8以上であって，係数が0である（変数は役に立つ）という仮説を棄却できない。したがって，これらのダミー変数はいずれも役に立たないと結論できる。

今回の解析結果では，方位や構造は家賃を決める要因になっていないようである。

間取りの追加

前例では，目的変数として，面積，築年数，駅歩，方位，構造を選択したが，方位，構造は役に立たなかった。今回は間取りに関するダミー変数を追加してみよう。

「駅徒歩分」の後に2列挿入し，「1K」，「1DK」というダミー変数を用意しよう。

分析ツールから回帰分析を行い，結果をみてみよう。

回帰係数推定結果

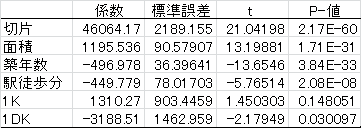
この結果を見ると最も家賃が高くなると思える1DKが他の間取りにくらべて，3,188円安いという直感に反する結果になってしまった（係数の符号が通常に考えられるものと逆である）。また，面積の係数は今までの解析結果では1050程度であったものが，1195へと変化し，10％以上高くなった（安定していた係数に急激な変化が生じた）。

これらの問題はなぜ起こったのだろうか。相関行列を見てみよう。

相関行列

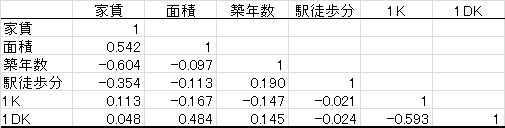
面積と1DKには高い相関が認められる。これが係数の符号が通常に考えられるものと逆になる原因である。

多重共線性

2つの説明変数の間に高い相関があったり，線形従属に近い説明変数の組合せがあったりする場合には，

といった好ましくない事態が発生することがある。このような問題を「多重共線性の問題」とよぶ。このような場合，互いに関係を持った説明変数の一部を除去するなど処置が必要である。

そこで，1DKを説明変数から抜いてみよう（1DKかどうかは面積でかなり決められるのだから）。

回帰係数推定結果

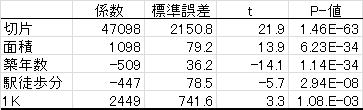
各説明変数のP値はいずれも十分に小さい値であり，すべての変数が家賃の予測に役立っているといえる。

家賃=47098＋1098×面積−509×築年数−447×駅歩+2449×1K
(t=21.9)(t=13.9)(t=-14.1)(t=-5.7)(t=3.3)

という回帰式が，われわれが得ることのできた最善のものとなった。

変数選択について

説明変数の候補として複数の変数があるとき，全ての変数を説明変数として使えば決定係数R2は最も高くなって，当てはまりは最良となる。しかし，その当てはまりの良さは，分析に用いたデータセットに対してだけ言えることであって，未知のデータセットに対しても有効とは限らない。特定のデータセットだけへの当てはまりを良くすると，他のデータセットへのあてはまりはかえって悪くなるのが普通である。 したがって，回帰式を作る場合には，有用なものを厳選して説明変数とする必要がある。

説明変数の候補としてk個の変数がある場合，考えられる重回帰式は2k-1通り存在する。kがある程度小さければ，全ての組合せについて試してみても良い（これを総当り法と呼ぶ）。

回帰式の良さの基準としては，自由度調整済み決定係数の他に，赤池のAIC（情報量基準）などが使われることがある。

総当りの法ができない場合には，次のような方法がある。

変数増加法
最初に最も予測に有効な独立変数（ 従属変数との相関係数が最も大きいもの ）を重回帰式に取り入れる。次の段階では，残りの独立変数の中で最も予測に有効な独立変数を取り入れる。予測精度の改善が一定限度以上である間，この操作を繰り返す。
変数減少法
最初に全ての独立変数を含む重回帰式を作る。次に，その中から最も予測に有効でない独立変数を除去する。予測精度の低下が一定限度以内である間，この操作を繰り返す。
変数増減法
変数増加法では，いったん重回帰式に取り込まれた独立変数は除去されることはないが，後の段階になってそれまでに取り込まれた独立変数の重要性が低くなることがある。変数増減法は各段階で変数を追加した後で除去すべき独立変数がないかをチェックする。
変数減増法
最初に全ての独立変数を含む重回帰式を作る。その後に続く各段階では，まず既に重回帰式に取り入れられている独立変数の中から最も予測に有効でない独立変数を除き，取り入れられていない独立変数の中に取り入れるべきものがないかをチェックする。

各変数の用不要の判定には，F値とよばれる統計量（＝ｔ値の2乗）が用いられることが多い。簡易的には，F値が2以上なら有効な変数，そうでなければ不要な変数とする方法が取られている。

統計解析ソフトは，このような方法を機械的に行ってくれるが，解析者が知識と経験を駆使して変数を選択するのが望ましい方法といえる。